El valor esperado y el manejo del riesgo y el tiempo del proyecto

Los métodos estadísticos, en especial las probabilidades, constituyen herramientas de gran utilidad en la gestión profesional de proyectos. Estas pueden ser aplicadas, entre otras áreas, en el manejo de la calidad, el tiempo y el riesgo de la iniciativa, facilitando la toma de decisiones en ambientes rodeados de incertidumbre.

Una de estas herramientas es el conocido valor esperado o esperanza matemática de una variable, que no es más que la media ponderada de los valores que tome dicha variable por sus respectivas probabilidades, esta puede ser formulada de la siguiente manera:

La esperanza matemática tiene aplicaciones tanto en el manejo del riesgo como en el del tiempo del proyecto, veamos a continuación ejemplos de ambos casos.

Aplicaciones en el manejo del riesgo

Supongamos que nos encontramos frente a un proyecto con cuatro posibles resultados, en lo referente a los beneficios que producirá. El primer escenario al que podemos definir como optimista nos indica que obtendremos un beneficio de 200 unidades monetarias, el segundo escenario moderado un beneficio de 100 unidades monetarias, el tercer escenario de equilibrio un beneficio de cero y el cuarto escenario pesimista una pérdida de 100 unidades monetarias.

Adicionalmente conocemos las probabilidades de que cada uno de estos escenarios se materialice, estás son 0,5, 0,2, 0,2 y 0,1 respectivamente. Calculemos entonces el valor esperado del beneficio del proyecto.

Una vez realizado el cálculo podemos concluir que en promedio el beneficio del proyecto será positivo lo que nos ayudaría a mitigar la incertidumbre sobre los valores que podría estar tomando esta variable en el futuro y facilitarnos, junto con otras herramientas de evaluación, el proceso de decisión sobre si ejecutar o no esta iniciativa. Debemos tener en cuenta que la esperanza matemática es un valor promedio de la variable en cuestión cuya probabilidad de ocurrencia es igual o muy cercana a cero, por lo que sería un error creer que el beneficio del proyecto será igual a 70 unidades monetarias.

Aplicaciones en el manejo del tiempo

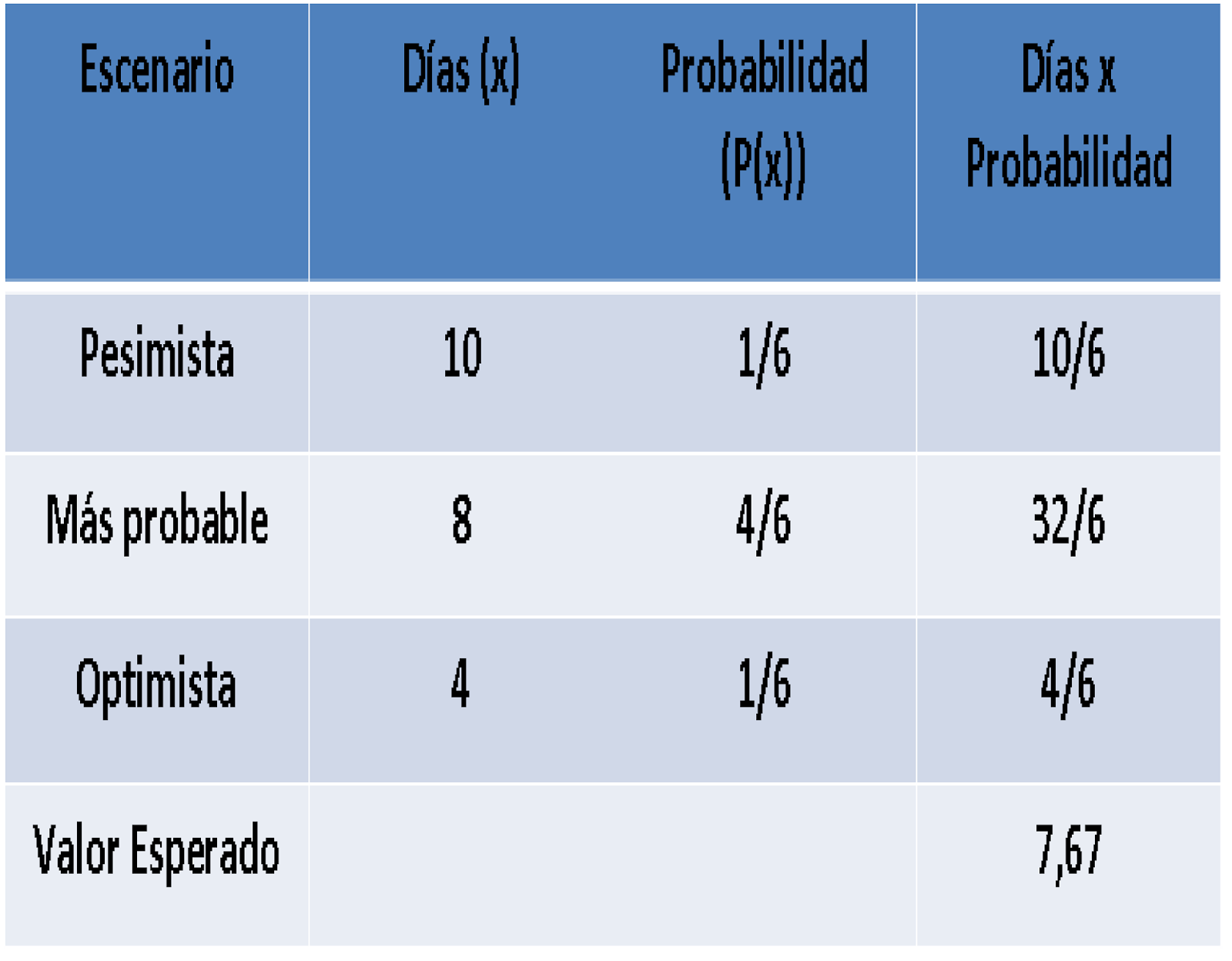
El tiempo esperado de duración de determinada actividad también puede ser pensado como un valor esperado. Supongamos que para la actividad A se nos plantean tres escenarios, uno pesimista igual a 10 días, uno más probable igual a 8 días y uno optimista igual a 4 días. Las probabilidades asociadas a cada unos de estos escenarios son 1/6, 4/6 y 1/6.

Realizando los cálculos como en el ejemplo anterior tendríamos:

En este caso el valor esperado para la duración de la actividad A es de 7,67 días en promedio.

El cálculo del valor esperado tiene una limitación y es que nos obliga a conocer de antemano las probabilidades, en caso de que no contemos con esta información tendremos que recurrir al uso de otros criterios que son: 

El criterio maximax que consiste en elegir aquella alternativa que nos proporcione el mayor beneficio o ganancia posible, según este criterio el decisor considera que la naturaleza siempre estará a su favor y se materializará el mejor escenario posible, en el caso del primer ejemplo esperaríamos obtener las 200 unidades monetarias de beneficio. 

El criterio maximin en este caso se elige la alternativa menos mala, entre aquellos estados de naturaleza poco favorables que se nos pueden presentar para la toma de decisiones.

Bibliografía consultada

Quantitative Methods for Project Management, escrito por el Dr. Frank T. Ambari, publicado por International Institute for Learning INC.